How to differentiate tan x the quotient rule can be used to differentiate tan x because of a basic quotient identity taken from trigonometry. Combining this formula with the pythagorean identity cos 2 θ sin 2 θ 1 two other forms appear.
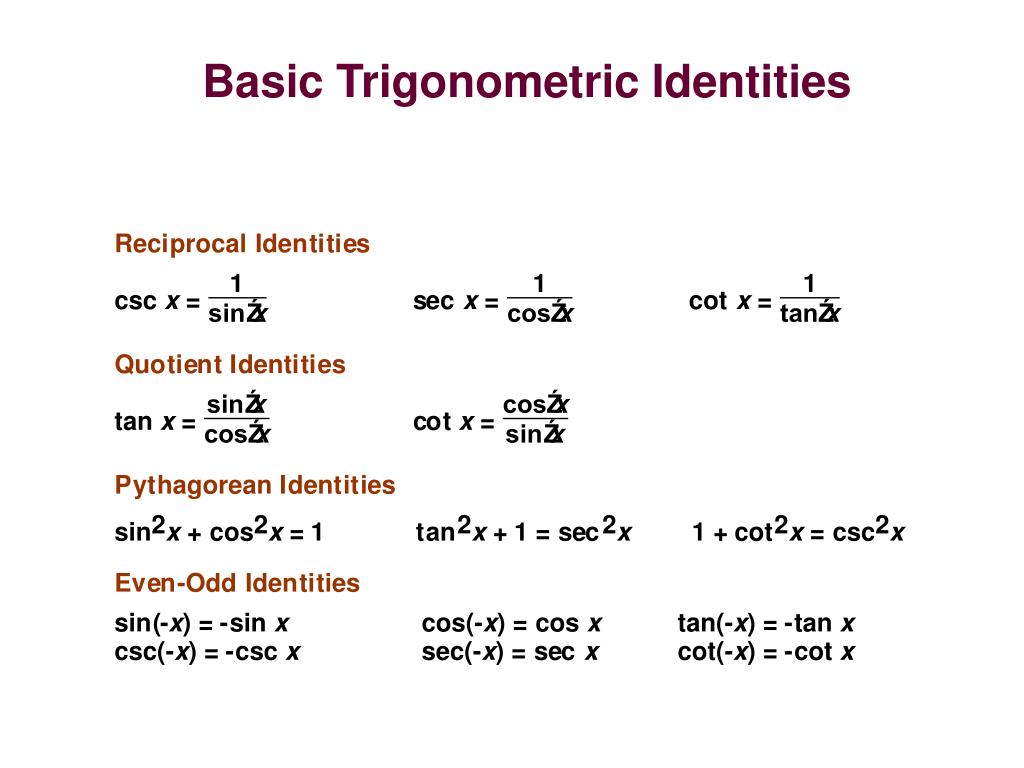Ppt Chapter 5 Verifying Trigonometric Identities Powerpoint Presentation Id 1294850
Formula 1 example and its solution.
Quotient identity example. This equation is always true. Let s look at the cotangent quotient identity using a familiar 45 45 90 triangle. Introduction a trigonometric function is appeared with another trigonometric function in division form in some cases but it is not always possible to divide a trigonometric function by.
1 1 the quotient identities will be used in trigonometric proofs and applications of calculus where using an identity is a more convenient form. The quotient r z is identified with the unit circle s1 r2 via trigonometry. Cotangent if you re unfamiliar with it is the inverse or reciprocal identity of tangent.
An identity is an equation that is always true. Show hide details. How to use the sine and cosine addition formulas to prove the double angle formulas.
There are two quotient identities that are crucial for solving problems dealing with trigs those being for tangent and cotangent. The solution is 7 x 3 2. How to use the quotient identity to solve the related problems.
In trigonometry quotient identities refer to trig identities that are divided by each other. Again consider the translation action on r by z. F x x 3 2 2x 1 1 x 3 2.
In this example those functions are 2x 1 and x 3. Found a content error. Cos 2θ 2cos 2 θ 1 and cos 2θ 1 2sin 2 θ.
The number 16 when divided by 3 has a quotient of 5 and the remainder as 1. A mathematical relation of two trigonometric functions in quotient form with another trigonometric function is called the quotient trigonometric identity. The derivation of the double angle identities for sine and cosine followed by some examples.
For t r we associate the point cos 2πt sin 2πt and this image point depends on exactly the z orbit of t i e t t0 r have the same image in the. The pythagorean identities the even odd identities the reciprocal identities and the quotient identities. Here when 35 7 the quotient would be 5 while 35 would be called the dividend and 7 the divisor.
Tan x sin x. Substitute the appropriate values into the identity and simplify. Solved example on quotient ques.
Tan θ sin θ cos θ is the quotient identity. In this first section we will work with the fundamental identities. What is the quotient of 27 3.
Step 4 use algebra to simplify where possible. Color highlighted text notes. We will begin with the pythagorean identities see table 1 which are equations involving trigonometric functions based on the properties of a right triangle.
Trig Identities Simplify Expressions Solutions Examples Videos
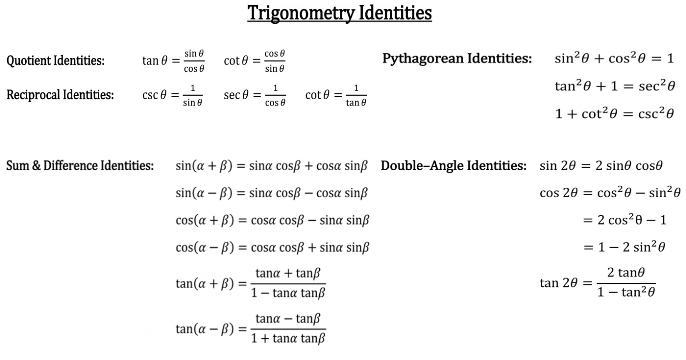How To Prove Quotient And Reciprocal Identities Studypug
Reciprocal Identities Quotient Identities And Pythagorean Identities With Worksheets Videos Games Activities
Chapter 6 Trigonometry 6 5 Basic Trigonometric Identities Ppt Video Online Download
Psk Lesson Notes Trig
Quotient Identity
Using Fundamental Identities Objectives 1 Recognize And Write The Fundamental Trigonometric Identities 2 Use The Fundamental Trigonometric Identities Ppt Download
0 komentar:
Posting Komentar